已知来自均匀分布总体U[0,1]的随机数为u,则用反函数法计算指数分布的随机数为( )。
A.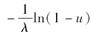
B.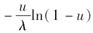
C.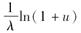
D.-λln(1-u)
E.λln(1+u)
参考答案与解析:
-
相关试题
-
已知来自均匀分布总体U[0,1]的随机数为u,则用反函数法计算指数分布的随机数为( )。
-
[单选题]已知来自均匀分布总体U[0,1]的随机数为u,则用反函数法计算指数分布的随机数为( )。A.B.C.D.-λln(1-u)E.λln(1+u)
- 查看答案
-
设已有[0,1]上均匀分布的随机数u,则用反函数法计算Weibull分布的随机数为( )。
-
[单选题]设已有[0,1]上均匀分布的随机数u,则用反函数法计算Weibull分布的随机数为( )。A.B.C.D.E.
- 查看答案
-
设已有[0,1]上均匀分布的随机数u,则用反函数法计算Weibull分布的随机数为( )。
-
[单选题]设已有[0,1]上均匀分布的随机数u,则用反函数法计算Weibull分布的随机数为( )。A.B.C.D.E.
- 查看答案
-
现有[0,1]上均匀分布的随机数:0.00582,0.00725,0.69011,0.25976,0.09763。利用反函数方法获得均值为1的泊松分布的随机数,则其对应的随机数为( )。
-
[单选题]现有[0,1]上均匀分布的随机数:0.00582,0.00725,0.69011,0.25976,0.09763。利用反函数方法获得均值为1的泊松分布
- 查看答案
-
现有[0,1]上均匀分布的随机数:0.00582,0.00725,0.69011,0.25976,0.09763。利用反函数方法获得均值为1的泊松分布的随机数,则其对应的随机数为( )。
-
[单选题]现有[0,1]上均匀分布的随机数:0.00582,0.00725,0.69011,0.25976,0.09763。利用反函数方法获得均值为1的泊松分布
- 查看答案
-
已知[0,1]区间上两个均匀分布的随机数u1=0.6341与u2=0.5791,则用Box-Muller方法生成的相应的标准正态分布的随机数分别为( )。
-
[单选题]已知[0,1]区间上两个均匀分布的随机数u1=0.6341与u2=0.5791,则用Box-Muller方法生成的相应的标准正态分布的随机数分别为(
- 查看答案
-
已知[0,1]区间上两个均匀分布的随机数u1=0.6341与u2=0.5791,则用Box-Muller方法生成的相应的标准正态分布的随机数分别为( )。
-
[单选题]已知[0,1]区间上两个均匀分布的随机数u1=0.6341与u2=0.5791,则用Box-Muller方法生成的相应的标准正态分布的随机数分别为(
- 查看答案
-
根据[0,1]区间上均匀分布的随机数列0.1247、0.9321和0.6873来表示Possion(3)的数,则Possion分布的随机数为( )。
-
[单选题]根据[0,1]区间上均匀分布的随机数列0.1247、0.9321和0.6873来表示Possion(3)的数,则Possion分布的随机数为( )。
- 查看答案
-
根据[0,1]区间上均匀分布的随机数列0.1247、0.9321和0.6873来表示Possion(3)的数,则Possion分布的随机数为( )。
-
[单选题]根据[0,1]区间上均匀分布的随机数列0.1247、0.9321和0.6873来表示Possion(3)的数,则Possion分布的随机数为( )。
- 查看答案
-
随机变量X的分布函数FX(x)是两个指数分布的综合,分布1是均值为1的指数分布,权重为0.25;分布2是均值为2的指数分布,权重为0.75。在[0,1]区间上均匀分布的随机数0.7来模拟X,则X为(
-
[单选题]随机变量X的分布函数FX(x)是两个指数分布的综合,分布1是均值为1的指数分布,权重为0.25;分布2是均值为2的指数分布,权重为0.75。在[0,1
- 查看答案
![已知来自均匀分布总体U[0,1]的随机数为u,则用反函数法计算指数分布的随机数为( )。 已知来自均匀分布总体U[0,1]的随机数为u,则用反函数法计算指数分布的随机数为( )。](https://img.zhaotiba.com/tiku83/16670906.jpg)