已知理赔总量S服从参数为N=12，p=0.25的二项分布，保险人会支付红利

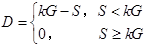
G为总保费，且已知k=0.8，G=5，则E（D）等于（　　）。[2008年真题]

[单选题]已知理赔总量S服从参数为N=12，p=0.25的二项分布，保险人会支付红利G为总保费，且已知k=0.8，G=5，则E（D）等于（　　）。[2008年真

[单选题]设聚合理赔S服从参数为λ=2的复合泊松分布，个别理赔额变量X的分布如下：则P/{S≤500/A.0.31B.0.45C.0.48D.0.50E.0.5

[单选题]设聚合理赔S服从参数为λ=2的复合泊松分布，个别理赔额变量X的分布如下：则P/{S≤500/A.0.31B.0.45C.0.48D.0.50E.0.5

[单选题]模拟一个复合分布的赔付。其中：（1）索赔次数N服从二项分布均值为8。（2）赔付额均匀分布于{1，2，3，4，5，6，7，8）。（3）赔付额相互独立，且

[问答题]设随机变量X服从于参数为（2 ，p）的二项分布，随机变量Y 服从于参数为（3 ，p）的二项分布，-------------.

[问答题]设随机变量X服从于参数为（2 ，p）的二项分布，随机变量Y 服从于参数为（3 ，p）的二项分布，-------------.

[单选题]模拟一个复合分布的赔付。其中：（1）索赔次数N服从二项分布均值为8。（2）赔付额均匀分布于{1，2，3，4，5，6，7，8）。（3）赔付额相互独立，且

[单选题]已知损失额X服从单参数的Pareto分布，其分布密度函数为：随机抽取5个样本，其中2个样本都超过了25，但具体数额未知，另外3个样本分别为3，6和14

[单选题]已知损失额X服从单参数的Pareto分布，其分布密度函数为：随机抽取5个样本，其中2个样本都超过了25，但具体数额未知，另外3个样本分别为3，6和14

[单选题]S服从复合泊松分布，泊松参数为λ=ln2，个体理赔额的概率函数为：则下面说法正确的是（　　）。A.S服从几何分布B.S服从二项分布C.S服从泊松分布D