设f(x)具有二阶连续导数,f(0)=0,f′(0)=0,f″(x)>0.在曲线y=f(x)上任意一点(x,f(x))(x≠0)处作此曲线的切线,次切线在x轴上的截距记为u,求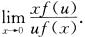
参考答案与解析:
-
相关试题
-
设f(x)具有二阶连续导数,f(0)=0,f′(0)=0,f″(x)>0.在曲线y=f(x)上任意一点(x,f(x))(x≠0)处作此曲线的切线,次切线在x轴上的截距记为u,求<img b
-
[问答题]设f(x)具有二阶连续导数,f(0)=0,f′(0)=0,f″(x)>0.在曲线y=f(x)上任意一点(x,f(x))(x≠0)处作此曲线的切线,次切
- 查看答案
-
设f(x)具有二阶连续导数,f(0)=0,f′(0)=0,f″(x)>0.在曲线y=f(x)上任意一点(x,f(x))(x≠0)处作此曲线的切线,次切线在x轴上的截距记为u,求<img b
-
[问答题]设f(x)具有二阶连续导数,f(0)=0,f′(0)=0,f″(x)>0.在曲线y=f(x)上任意一点(x,f(x))(x≠0)处作此曲线的切线,次切
- 查看答案
-
设f′(x0)=f″(x0)=0,f′″(x0)>0,且f(x)在x0点的某邻域内有三阶连续导数,则下列选项正确的是( ).
-
[单选题]设f′(x0)=f″(x0)=0,f′″(x0)>0,且f(x)在x0点的某邻域内有三阶连续导数,则下列选项正确的是( ).A.B.C.D.
- 查看答案
-
设f′(x0)=f″(x0)=0,f′″(x0)>0,且f(x)在x0点的某邻域内有三阶连续导数,则下列选项正确的是( ).
-
[单选题]设f′(x0)=f″(x0)=0,f′″(x0)>0,且f(x)在x0点的某邻域内有三阶连续导数,则下列选项正确的是( ).A.B.C.D.
- 查看答案
-
设f′(x0)=f″(x0)=0,f′″(x0)>0,且f(x)在x0点的某邻域内有三阶连续导数,则下列选项正确的是( ).
-
[单选题]设f′(x0)=f″(x0)=0,f′″(x0)>0,且f(x)在x0点的某邻域内有三阶连续导数,则下列选项正确的是( ).A.B.C.D.
- 查看答案
-
设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。
-
[单选题]设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。A
- 查看答案
-
设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。
-
[单选题]设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。A
- 查看答案
-
设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。
-
[单选题]设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。A
- 查看答案
-
设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。
-
[单选题]设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。A
- 查看答案
-
设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。
-
[单选题]设曲线积分∫l[f(x)-ex]sinydx-f(x)cosydy与路径无关,其中f(x)具有一阶连续导数,且f(0)=0,则f(x)等于( )。A
- 查看答案
