.设方程组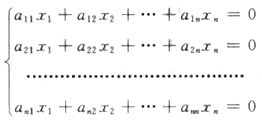的系数行列式|A|=0，而|A|中的某个元素aij的代数余子式Aij≠0.

[问答题]设方程组为非齐次的（即至少有一个bi≠0），且系数矩阵的秩为r，证明：若方程组（Ⅰ）有解，则有n-r+1个解向量线性无关，且（Ⅰ）的每个解向量都可由它

[问答题]设x≥0，证明：

[问答题]设有方程组

[问答题]设线性方程组，试就λ、μ讨论方程组的解的情况，有解时求出其解。

[问答题]证明方程组的解全是方程（Ⅱ）b１ｘ１＋b２ｘ２＋…＋bｎｘｎ＝０的解的充分必要条件是：向量β＝（b１，b２，…，bｎ）可由向量组α1，α2，…，αs线

[问答题]设函数y=y（x）由方程组确定，求

[问答题]设四元线性齐次方程组（Ⅰ）为又已知某线性齐次方程组（Ⅱ）的通解为：k1（0，1，1，0）T+k2（-1，2，2，1）T.（1）求线性方程组（Ⅰ）的基础

[问答题]设总体X的分布密度（X1，X2，…，Xn）为其样本，求a参数的矩估计量与极大似然估计量。现得样本值为0.1，0.2，0.9，0.8，0.7，0.7，求

[问答题]求极限

[问答题]求极限