设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数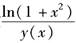
的极限（ ）。
A.不存在
B.等于1
C.等于2
D.等于3
参考答案与解析：
-
相关试题
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
-
设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数<img border="0" style=&quo
-
[单选题]设y=y（x）是二阶常系数微分方程y″+py′+qy=e3x满足初始条件y（0）=y′（0）=0的特解，则当x→0时，函数的极限（ ）。A.不存在B
- 查看答案
