案例：某学校的初二年级数学备课组针对“一次函数”，拟对“兴趣班”的学生上一次拓展课，经过讨论，拟定了如下教学目标：
①进一步理解一次函数解析式y=kx+b(k≠0)中参数的含义；
②探索两个一次函数图像的位置关系。
为了落实教学目标②，针对参数k，甲.乙两位老师给出了不同的教学思路：
【教师甲】
先出示问题：一次函数图像是直线，两个一次函数表示的直线平行时，它们对应的一次函数解析式中参数k有什么特点呢
然后。给出一般结论：若函数y=k1x+b1(k1≠0)，y=kg+b2(k2≠0)表示的两条直线平行，则有k1=k2。接着通过具体实例，让学生体会参数k的含义。
【教师乙】
让学生在同一坐标系下，作一次函数图像，在此过程中体会k的含义。如，将学生分两组，

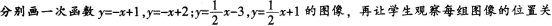
系，从而体会参数k的含义。
问题：
(1)对该备课组拟定的教学目标进行评析；(6分)
(2)分析甲.乙两位教师教学思路的特点。(14分)

[单选题]已知一次函数y=kx-k，若y随着x的增大而减小，则该函数图像经过（）。A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象

[单选题]已知一次函数y=kx-k，若y随着x的增大而减小，则该函数图像经过（）。A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象

[主观题]如图，直线l是一次函数 y=kx+b 的图像，求k与b的值。

[主观题]已知一次函数的图象经过点A（2，1），B（－1，－3）（1）求此一次函数的解析式；（2）求此一次函数的图象与x轴、y轴的交点坐标；（3）求此一次函数的图象与两坐标轴所围成的三角形面积。

[主观题]数学理解有一组数同时适合方程 x+y=2和 x+y=5吗？一次函数y=2-x，y=5-x的图像之间有何关系？你能从中“悟”出些什么吗？

[主观题]下图中，表示一次函数的有哪些？

[单选题]一次函数y1=kx+b与y2=x+a的图象如图，则下列结论：①k<0；②a>0；③当x<3时，y1A.0B.1C.2D.3

[单选题]若m+n＜0，mn＞0，则一次函数y=mx+n的图像不经过（）。A.第一象限B.第二象限C.第三象限D.第四象限E.第一、三象限

[单选题]若m+n＜0，mn＞0，则一次函数y=mx+n的图像不经过（）。A.第一象限B.第二象限C.第三象限D.第四象限E.第一、三象限

[单选题]若一次函数y=（3-k）x-k的图像经过第二、三、四象限，则k的取值范围是（）。A.k＞3B.0＜k≤3C.0≤k＜3D.0＜k＜3E.k＞0