设某运输车队每年大约事故发生次数服从泊松分布，参数λ可取0或5，又设λ的先验分布为:P（λ=0）=0.4，P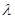（=5）=0.6。假如某一年该车队发生了三次事故，则λ的期望为（　　）。

[单选题]某险种的年索赔次数服从参数为λ的泊松分布，参数λ的先验分布如下：假设第一年某保单发生10次索赔，则该保单在第二年索赔次数的Bayes信度估计值为（　　

[问答题]设总体X～P（λ）（即X服从于参数为λ的泊松分布），其中λ>0.是来自总体的简单随机样本，证明：

[问答题]设总体X～P（λ）（即X服从于参数为λ的泊松分布），其中λ>0.是来自总体的简单随机样本，证明：

[单选题]设聚合理赔S服从参数为λ=2的复合泊松分布，个别理赔额变量X的分布如下：则P/{S≤500/A.0.31B.0.45C.0.48D.0.50E.0.5

[单选题]设聚合理赔S服从参数为λ=2的复合泊松分布，个别理赔额变量X的分布如下：则P/{S≤500/A.0.31B.0.45C.0.48D.0.50E.0.5

[问答题]设X和Y相互独立，X服从参数为λ的泊松分布，其分布率为，其中λ>0，

[问答题]设X和Y相互独立，X服从参数为λ的泊松分布，其分布率为，其中λ>0，

[单选题]假设一个健康险的分布为符合泊松分布，索赔次数服从Possion（3），每次索赔额服从的分布函数为单位为万元。根据[0，1]区间上均匀分布R的随机数列0

[单选题]假设一个健康险的分布为符合泊松分布，索赔次数服从Possion（3），每次索赔额服从的分布函数为，单位为万元。根据[0，1]区间上均匀分布R的随机数列

[单选题]设索赔频率q服从以a，b为参数的贝塔分布，其先验分布的密度函数为（0，1）上均匀分布，即，，，。在已知的条件下，每份保单的索赔次数服从参数为θ的二项分