当前位置：找题吧 > 军队文职档案类

[单选题]

设函数f(x)在闭区间[a，b]上有定义，在开区间(a，b)内可导，则（）。

A.当f(a)f(b)＜0时，存在ξ∈(a，b)，使f(ξ)=0

B.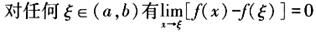

C.当f(a)=f(b)时，存在ξ∈(a，b)，使f′(ξ)=0

D.存在ξ∈(a，b)，使f(b)-f(a)=f′(ξ)(b-a)

参考答案与解析：

相关试题

设函数f（x）在闭区间[a，b]上有定义，在开区间（a，b）内可导，则（　　）.: [单选题]设函数f（x）在闭区间[a，b]上有定义，在开区间（a，b）内可导，则（　　）.A.B.C.D.

查看答案

设函数f（x）在闭区间[a，b]上有定义，在开区间（a，b）内可导，则（　　）.: [单选题]设函数f（x）在闭区间[a，b]上有定义，在开区间（a，b）内可导，则（　　）.A.B.C.D.

查看答案

设函数f（x）在闭区间[a，b]上有定义，在开区间（a，b）内可导，则（　　）.: [单选题]设函数f（x）在闭区间[a，b]上有定义，在开区间（a，b）内可导，则（　　）.A.B.C.D.

查看答案

设函数f(x)在闭区间[a，b]上有定义，在开区间(a，b)内可导，则（）。: [单选题]设函数f(x)在闭区间[a，b]上有定义，在开区间(a，b)内可导，则（）。A.当f(a)f(b)＜0时，存在ξ∈(a，b)，使f(ξ)=0B.C.当

查看答案

设不恒为常数的函数f（x）在闭区间[a,b]上连续，在开区间（a,b）内可导，且f（a）=f（b）.证明：在（a,b）内至少存在一点ξ，使得f′（ξ）>0.: [问答题]设不恒为常数的函数f（x）在闭区间[a,b]上连续，在开区间（a,b）内可导，且f（a）=f（b）.证明：在（a,b）内至少存在一点ξ，使得f′（ξ）

查看答案

设不恒为常数的函数f（x）在闭区间[a,b]上连续，在开区间（a,b）内可导，且f（a）=f（b）.证明：在（a,b）内至少存在一点ξ，使得f′（ξ）>0.: [问答题]设不恒为常数的函数f（x）在闭区间[a,b]上连续，在开区间（a,b）内可导，且f（a）=f（b）.证明：在（a,b）内至少存在一点ξ，使得f′（ξ）

查看答案

设不恒为常数的函数f（x）在闭区间[a,b]上连续，在开区间（a,b）内可导，且f（a）=f（b）.证明：在（a,b）内至少存在一点ξ，使得f′（ξ）>0.: [问答题]设不恒为常数的函数f（x）在闭区间[a,b]上连续，在开区间（a,b）内可导，且f（a）=f（b）.证明：在（a,b）内至少存在一点ξ，使得f′（ξ）

查看答案

设函数f（x）在闭区间[0,1]上连续，在开区间（0,1）内可导，且f（0）=0,f（1）=<img border="0" style="width: 15px;: [问答题]设函数f（x）在闭区间[0,1]上连续，在开区间（0,1）内可导，且f（0）=0,f（1）=,证明：存在

查看答案

设函数f(x)在区间(0，1)内可导，f′(x)＞0，则在(0，1)内f(x)().: [单选题]设函数f(x)在区间(0，1)内可导，f′(x)＞0，则在(0，1)内f(x)().A.单调增加B.单调减少C.为常量D.既非单调，也非常量

查看答案

罗尔定理：设函数(x)满足条件：(1)在闭区间[a，b]上连续；(2)在开区间(a，b)内可导；(3)(a)=(b)，则在(a，b)内至少存在一点ξ，使得，′(ξ)=0。证明这个定理并说明其几何意义。: [问答题]罗尔定理：设函数(x)满足条件：(1)在闭区间[a，b]上连续；(2)在开区间(a，b)内可导；(3)(a)=(b)，则在(a，b)内至少存在一点ξ，

查看答案