[问答题]
(本题满分10分)
数列{xn},x1>0,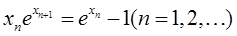 。证:{xn}收敛,并求
。证:{xn}收敛,并求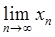 。
。
参考答案与解析:
-
相关试题
-
(本题满分10分)<br /> 数列{xn},x1>0,<img border="0" style="width: 275px; height: 38
-
[问答题](本题满分10分) 数列{xn},x1>0,。证明{xn}收敛,并求。
- 查看答案
-
(本题满分11分)数列{xn},x1>0,<img border="0" style="width: 129px; height: 35px;" src=
-
[问答题](本题满分11分)数列{xn},x1>0,(n=1,2,…)证明{xn}收敛,并求。
- 查看答案
-
(本题满分10分)<br />求数列极限<img border="0" style="width: 119px; height: 44px;"
-
[问答题](本题满分10分)求数列极限。
- 查看答案
-
(本题满分10分)<br />设<img border="0" style="width: 36px; height: 21px;" src=
-
[问答题](本题满分10分)设在上可导且。证明:存在,使。
- 查看答案
-
(本题满分10分)<br /> 设函数<img border="0" style="width: 36px; height: 21px;"
-
[问答题](本题满分10分) 设函数在定义域上的导数大于零,若对任意,曲线在点处的切线与直线及轴所围成区域的面积恒为4,且,求表达式。
- 查看答案
-
(本题满分10分)设数列{an}满足条件:<br /><img border="0" style="width: 247px; height: 23px
-
[问答题](本题满分10分)设数列{an}满足条件:S(x)是幂级数(1)证明:(2)求S(x)的表达式。
- 查看答案
-
(本题满分10分)<br />设函数<img border="0" style="width: 36px; height: 22px;" sr
-
[问答题](本题满分10分)设函数在内可导与是内的两点,由下式定义:证明:对与之间的任何值,在与之间至少存在一点使.
- 查看答案
-
(本题满分10分)<br /> (Ⅰ)设函数<img border="0" style="width: 36px; height: 27px;&quo
-
[问答题](本题满分10分) (Ⅰ)设函数,可导,利用导数定义证明。 (Ⅱ)设函数,,…,可导,,写出的求导公式。
- 查看答案
