[问答题]
(本题满分10分)
(1)求证:对任何0<|x|≤1,存在θ(x)∈(0,1),使得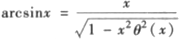 .
.
(2)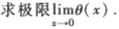
参考答案与解析:
-
相关试题
-
(本题满分10分)<br />设f(x)在[0,1]上可导,且f(0)=0,又f(x)满足关系<img border="0" style="width:
-
[问答题](本题满分10分)设f(x)在[0,1]上可导,且f(0)=0,又f(x)满足关系=25,求f(x).
- 查看答案
-
(本题满分10分)<br />设f(x)在[0,1]上连续.<br />(Ⅰ)证明至少存在一个<img border="0" style="
-
[问答题](本题满分10分)设f(x)在[0,1]上连续.(Ⅰ)证明至少存在一个∈(0,1),使得;(Ⅱ)若f(x)为可导函数且满足(1-x)(x)﹥2f(x)
- 查看答案
-
(本题满分10分)<br />设函数f(x)在区间[0,1]上具有连续导数,f(0)=1,且满足<img border="0" style="width
-
[问答题](本题满分10分)设函数f(x)在区间[0,1]上具有连续导数,f(0)=1,且满足其中求f(x)的表达式.
- 查看答案
-
(本题满分10分)<br /> 数列{xn},x1>0,<img border="0" style="width: 237px; height: 36
-
[问答题](本题满分10分) 数列{xn},x1>0,。证:{xn}收敛,并求。
- 查看答案
-
(本题满分10分)<br /> 数列{xn},x1>0,<img border="0" style="width: 275px; height: 38
-
[问答题](本题满分10分) 数列{xn},x1>0,。证明{xn}收敛,并求。
- 查看答案
-
(本题满分10分)<br />已知函数f(x,y)具有二阶连续偏导数,且f(1,y)=0,f(x,1)=0,<img border="0" style="
-
[问答题](本题满分10分)已知函数f(x,y)具有二阶连续偏导数,且f(1,y)=0,f(x,1)=0,,其中D={(x,y)︱0≤x≤1,0≤Y≤1),计算
- 查看答案
-
(本题满分11分)数列{xn},x1>0,<img border="0" style="width: 129px; height: 35px;" src=
-
[问答题](本题满分11分)数列{xn},x1>0,(n=1,2,…)证明{xn}收敛,并求。
- 查看答案
-
若在[0,1]上有f(0)=g(0)=0,f(1)=g(1)=a>0,且f″(x)>0,g″(x)<0,则<img border="0" style=&qu
-
[单选题]若在[0,1]上有f(0)=g(0)=0,f(1)=g(1)=a>0,且f″(x)>0,g″(x)<0,则的大小关系是( ).A.B.C.D.
- 查看答案
-
(本题满分11分)<br /> 已知总体X的密度函数为<br /><img border="0" style="width: 255px;
-
[问答题](本题满分11分) 已知总体X的密度函数为 其中σ∈(0,+∞)为未知参数,为来自总体X的简单随机样本,记σ的最大似然估计量为。 (I)求;
- 查看答案
-
(本题满分11分)<br /> 已知总体X的密度函数为<br /><img border="0" style="width: 279px;
-
[问答题](本题满分11分) 已知总体X的密度函数为 其中σ∈(0,+∞)为未知参数,X1,X2,…,Xn为来自总体X的简单随机样本,记σ的最大似然估计量为
- 查看答案
