级数前几项和s_n=a₁+a₂+…+a_n，若a_n≥0，判断数列｛s_n｝有界是级数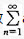a_n收敛的什么条件（）？

[单选题]在数列an (n=1,2,……)中，a1 =1959，a2 =1995，且从第三项开始，每项是它前两项的平均数的整数部分，则=A . 1980B . 1981C . 1983D . 1982

[问答题]设数列{an}的前n项和为Sn，且an+Sn=1(n∈N*)。(1)求{an}的通项公式；(2)若数列{bn}满足b1=1，且2bn+1=bn+an(

an=2n+1(当n为奇数)an=2∧n (当n为偶数)要求n项的和必须n为连续自然数;所以 设奇数n=2m-1;偶数n=2m.（m为连续自然数）所以1、奇数项:an=2n+1=2(2m-1)+1=4m-1；Sn1＝（3＋4m-1）*m/2=（4m+2）*m/2=（2m+1）*m将m用n复原：m＝（n+1）/2Sn1＝（2（n+1）/2+1）*（n+1）/2＝（n+1）（n+2）/22、偶数项an=2n=2∧2m=4∧mSn2＝4*(4m-1)/(4-1)= 4*(4m-1)/3。将m用n复原：m＝n/2

[问答题](10分)已知数列{an}的前n项和Sn=2n+1-k(其中k为常数)：(1)求数列{an}的通项公式；(4分)(2)若a1=2，求数列{nan}的前

[问答题](10分)已知数列{an}满足a1=3，an+1=an+2n，(1)求{an}的通项公式an；(2)若bn=nan，求数列{bn}的前n项和sn。

[问答题] 设数列｛an｝前n项和为Sn，且an+Sn=1（n∈N*）（1）求｛an｝的通项公式；（2）若数列｛bn｝满足b1=1且2bn+1=bn+an（n≥1），求数列｛bn｝的通项公式。

[问答题] 数列{an}的前n项和Sn=2n-an，先计算数列的前4项，后猜想an并证明之。

[单选题]幂级数x2-（1／3）x3+（1／3）x4-…+[（-1）n+1／n]xn+1+…（-1（）A . xsinxB . x2／（1+x2）C . x1n（1-x）D . x1n（1+x）

[单选题]若，则在S1，S2，……，S100中，正数的个数是（）。A . 16B . 72C . 86D . 100

[主观题]设Sn为等差数列｛an｝的前n项和，若S3=3，S6=24，则a9= 。